รังสีเอกซ์ (X-ray หรือ Röntgen ray) เป็นรังสีแม่เหล็กไฟฟ้า ที่มีความยาวคลื่นในช่วง 10 ถึง 0.01 นาโนเมตร ตรงกับความถี่ในช่วง 30 ถึง 30,000 พีต้าเฮิตซ์ (1015 เฮิตซ์) ในเบื้องต้นมีการใช้ช้รังสีเอกซ์สำหรับถ่ายภาพเพื่อการวินิจฉัยโรค และงานผลึกศาสตร์(crystallography) รังสีเอกซ์เป็นการแผ่รังสีแบบแตกตัวเป็นไอออน และมีอันตรายต่อมนุษย์ รังสีเอกซ์ค้นพบโดยวิลเฮล์ม คอนราด เรินต์เกนเมื่อ ค.ศ. 1895
ทฤษฎีอิเล็กตรอนสมัยปัจจุบัน อธิบายถึงการเกิดรังสีเอกซ์ว่า ธาตุประกอบด้วยอะตอมจำนวนมากในอะตอมแต่ละตัวมีนิวเคลียสเป็นใจกลาง และมีอิเล็กตรอนวิ่งวนเป็นชั้นๆ ธาตุเบาจะมีอิเล็กตรอนวิ่งวนอยู่น้อยชั้น และธาตุหนักจะมีอิเล็กตรอนวิ่งวนอยู่หลายชั้น เมื่ออะตอมธาตุหนักถูกยิงด้วยกระแสอิเล็กตรอน จะทำให้อิเล็กตรอนที่อยู่ชั้นในถูกชนกระเด็นออกมาวิ่งวนอยู่รอบนอกซึ่งมีภาวะไม่เสถียรและจะหลุดตกไปวิ่งวนอยู่ชั้นในอีก พร้อมกับปล่อยพลังงานออกในรูปรังสี ถ้าอิเล็กตรอนที่ยิงเข้าไปมีพลังงานมาก ก็จะเข้าไปชนอิเล็กตรอนในชั้นลึกๆ ทำให้ได้รังสีที่มีพลังงานมาก เรียกว่า ฮาร์ดเอกซเรย์ (hard x-ray) ถ้าอิเล็กตรอนที่ใช้ยิงมีพลังงานน้อยเข้าไปได้ไม่ลึกนัก จะให้รังสีที่เรียกว่า ซอฟต์เอกซเรย์ (soft x-ray)
กระบวนการเกิดหรือการผลิตรังสีเอกซ์ทั้งโดยฝีมือมนุษย์และในธรรมชาติ มีอยู่ 2 วิธีใหญ่ๆ คือ วิธีที่ 1 เป็นวิธีผลิตรังสีเอกซ์โดยการยิงลำอนุภาคอิเล็กตรอนใส่แผ่นโลหะ เช่น ทังสเตน อิเล็กตรอน ที่เป็นกระสุนจะวิงไปชนอิเล็กตรอนของอะตอมโลหะที่เป็นเป้า ทำให้อิเล็กตรอนที่ถูกชนเปลี่ยนตำแหน่ง การโคจรรอบนิวเคลียส เกิดตำแหน่งที่ว่างของอิเล็กตรอนในวงโคจรรอบนิวเคลียสเดิม อิเล็กตรอนตัวอื่นที่ อยู่ในตำแหน่งวงโคจรมีพลังงานสูงกว่า จะกระโดดเข้าไปแทนที่ของอิเล็กตรอนเดิมแล้วปล่อยพลังงานออก มาในรูปของคลื่นแม่เหล็กไฟฟ้าคือ รังสีเอกซ์ เครื่องฉายรังสีเอกซ์ที่ใช้งานกันทั่วไปในโรงพยาบาลและในโรงงานอุตสาหกรรม ล้วนเป็นเครื่องผลิต รังสีเอกซ์จากวิธีการนี้ วิธีที่ 2 เป็นวิธีผลิต หรือ กำเนิดรังสีเอกซ์จากการเคลื่อนที่ของอนุภาคที่มีประจุไฟฟ้า เช่น อิเล็กตรอน โปรตอนหรืออะตอม อย่างมีความเร่ง คือ อนุภาคที่มีประจุไฟฟ้าเหล่านี้เคลื่อนที่ด้วยความเร็วสูงขึ้นแล้วก็เป็น ธรรมชาติของอนุภาคที่มีประจุไฟฟ้าเหล่านี้เอง ที่ต้องปล่อยพลังงานออกมาในรูปของ คลื่นแม่เหล็กไฟฟ้า อย่างที่ไม่มีอะไรไปห้ามได้ ซึ่งถ้าคลื่นแม่เหล็กไฟฟ้าที่ถูกปล่อยออกมามีความถี่สูงพอก็จะเป็นรังสีเอกซ์ กำเนิดรังสีเอกซ์วิธีนี้เป็นวิธีที่นักวิทยาศาสตร์ที่นิยมใช้ในการผลิตรังสีเอกซ์ในห้องทดลองวิทยาศาสตร์
ประวัติศาสตร์ในการศึกษารังสีเอกซ์[แก้]
Johann Hittorf (1824 - 1914) นักฟิสิกส์ที่ทำการศึกษารังสีพลังงานสูงที่ปลดปล่อยออกมาจากขั้วลบในท่อเอกซเรย์ รังสีนี้มีความเรืองแสงเมื่อกระทบหลอดแก้วของท่อเอกซเรย์ ในปี 1876 Eugen Goldstein ได้เรียกปรากฏการณ์นี้ว่า รังสีแคโทด ซึ่งเป็นที่รู้จักกันในปัจจุบันว่าคือ กระแสอิเล็กตรอน ต่อมา นักฟิสิกส์ชาวอังกฤษ William Crookes ได้ทำการศึกษาผลของกระแสอิเล็กตรอนในความดันที่ต่ำ และก็ได้เรียกสิ่งที่เขาค้นพบว่า Crookes tube ซึ่งเป็นท่อแก้วสุญญากาศ มีขั้วอิเล็กโทรดแรงเคลื่อนไฟฟ้าสูง โดยเขาได้ทดลองนำแผ่นถ่ายภาพไว้ข้างท่อแก้ว พบว่าเกิดรอยดำบนแผ่น แต่ Crookes ยังไม่ได้อธิบายปรากฏการณ์นี้
ในเดือนเมษายนปี 1887 Nikola Tesla ได้เริ่มทำการศึกษารังสีเอกซ์โดยใช้ท่อสุญญากาศแรงเคลื่อนไฟฟ้าสูงที่เขาคิดค้นขึ้นเอง (เช่นเดียวกับ Crookes tube) จากวารสารตีพิมพ์ต่าง ๆ ได้บ่งชี้ว่า เขาได้เป็นผู้พัฒนาท่อเอกซเรย์ขึ้น ซึ่งแตกต่างจากท่อเอกซเรย์อื่น ๆ ที่มีขั้วอิเล็กโทรดเพียงด้านเดียว
โดยหลักการของ Tesla ที่ได้พัฒนาท่อเอกซเรย์ขึ้นมา ในปัจจุบันเรียกว่ากระบวนการ Bremsstrahlung ซึ่งเป็นกระบวนการที่รังสีเอกซเรย์ที่ถูกปลดปล่อยออกมานั้นเกิดจากการเร่งประจุเช่นอิเล็กตรอนในวิ่งผ่านสสารบางชนิด ในปี 1892 Tesla ได้ทำเสนอผลการทดลองซึ่งเขายังเรียกเพียงว่าเป็นพลังงานจากการแผ่รังสี ในตอนนั้นเขายังไม่ได้เสนอผลการทดลองให้เป็นที่กว้างขวางมากนัก แต่ผลจากการทดลองของเขาส่งผลต่อวงการวิทยาศาสตร์และทางการแพทย์ในปัจจุบันอย่างมาก
ในปี 1892 Heinrich Hertz ได้ทำการทดลองกับรังสีแคโทดรวมกับแผ่นโลหะบาง (เช่น อะลูมิเนียม) ต่อมา Philipp Lenard นักศึกษาของ Hertz ได้ทำการวิจัยปรากฏการณ์นี เขาได้พัฒนาท่อแคโทดขึ้นใหม่และใช้วัสดุหลายชนิดในการเป็นตัวกลาง เขาไม่ได้ตระหนักเลยว่า นั่นคือการสร้างรังสีเอกซ์ ต่อมา Hermann von Helmholtz ได้ทำการศึกษาสมการทางคณิตศาสตร์ของรังสีเอกซ์ เขาได้ตั้งสมมุติฐานก่อนที่ R?ntgen จะค้นพบและพิสูจน์ได้ ซึ่งต่อมาเป็นรากฐานของทฤษฎีทางคลื่นแม่เหล็กไฟฟ้า
ในวันที่ 8 พฤศจิกายน 1896 Wilhelm Conrad R?ntgen นักฟิสิกส์ชาวเยอรมัน ได้เริ่มทำการศึกษาและวิจัยรังสีเอกซ์ขณะทำการทดลองกับท่อสุญญากาศ แล้วในวันที่ 28 ธันวาคม 1895 เขาได้เขียนรายงานเรื่อง On a new kind of ray: A preliminary communication ซึ่งรายงานเล่มนี้ได้พูดถึง รังสี x ซึ่งได้ระบุไว้ว่าเป็นรังสีที่ยังระบุประเภทไม่ได้ (จึงตั้งชื่อไว้ก่อนว่า รังสี x) ส่งผลให้ชื่อรังสีเอกซ์ถูกใช้กันมานิยมมากกว่าชื่อที่นักวิทยาศาสตร์ตั้งให้ว่า รังสีเรินต์เก้น (R?ntgen rays) และทำให้ R?ntgen ได้รับรางวัลโนเบลสาขาฟิสิกส์จากการค้นพบและพิสูจน์ปรากฏการณ์นี้
ในการทดลองของ R?ntgen ได้เริ่มจากการใช้เครื่องสร้างรังสีแคโทดผ่านท่อแก้วสุญญากาศ เขาได้พบว่ามีแสงสีเขียวอ่อนวิ่งปะทะกับผนังท่อ เขาได้พบว่า แสงจากเครื่องสร้างรังสีแคโทดนี้ได้ทะลุผ่านวัสดุต่าง ๆ (เช่น กระดาษ ไม้ หนังสือ) เขาได้เริ่มวางวัตถุอื่น ๆ หลายประเภทไว้หน้าเครื่องนี้ และทำให้เขาได้พบว่า เขาสามารถถ่ายเห็นโครงร่างของกระดูกมือของเขาได้บนผนัง สองเดือนต่อมาเขาเริ่มทำการค้นคว้า และได้ทำการพิสูจน์และตีพิมพ์ในปี 1896 ในรายงานชื่อ On a New Kind of Radiation
ย้อนกลับไปในปี 1985 Thomas Edison ก็ได้ทำการศึกษาผลของวัสดุหลายประเภทที่เรืองแสงได้ด้วยรังสีเอกซ์ และได้พบ calcium tungstate ซึ่งเป็นวัสดุที่ดีที่สุด ในเดือนมีนาคม ปี 1896 ได้ริเริ่มพัฒนากล้องตรวจอวัยวะภายในด้วยเงารังสีเอกซ์บนจอเรืองแสง (fluoroscope) ซึ่งมีใช้กันแพร่หลายในปัจจุบัน แม้ว่า Edison จะหยุดการวิจัยเกี่ยวกับรังสีเอกซ์ในปี 1903 หลังจากการจากไปของ Clarence Madison Dally ซึ่งเป็นช่างเป่าแก้วของเขา Dally ในตอนนั้นมีนิสัยชอบทดสอบท่อรังสีเอกซ์ด้วยมือเปล่า เขาได้เริ่มเป็นมะเร็งและจำเป็นต้องตัดมือทั้งสองข้างก่อนที่จะเสียชีวิต
ในปี 1906 Charles Barkla ได้ค้นพบว่า รังสีเอกซ์สามารถถูกกระเจิงได้ด้วยก๊าซ และได้บอกว่าวัตถุใดที่มีคุณสมบัติเช่นนี้จะมีลักษณะเช่นเดียวกับรังสีเอกซ์ (characteristic x-ray) เขาได้รับรางวัล Nobel prize ในปี 1917 จากการค้นพบสิ่งนี้
ในปี 1912 Max von Laue, Paul Knipping and Walter Friedrich ได้ทำการค้นคว้าการเบี่ยงเบนของรังสีเอกซ์ด้วยคริสตัล การทดลองนี้ เป็นจุดเริ่มต้นของสาขา X-ray crystallography ที่มีนักฟิสิกส์ Paul Peter Ewald, William Henry Bragg and William Lawrence Bragg ได้วางรากฐานและพัฒนาต่อม
ในการประยุกต์ใช้รังสีเอกซ์ทางการแพทย์นั้น (radiation therapy) ได้เริ่มต้นโดย Major John Hall-Edwards นักฟิสิกส์ชาวอังกฤษ ในปี 1908 เขาจำเป็นต้องเสียแขนซ้ายด้วยผลของการแผ่รังสีเอกซ์ และในปี 1950 ได้กล้องถ่ายภาพเอกซเรย์ (x-ray microscope) ได้พัฒนาขึ้นสำเร็จ
ในปี 1980 เลเซอร์รังสีเอกซ์ (x-ray laser) ถูกนำมาใช้ในส่วนหนึ่งของแผนการป้องกันของรีแกน (Reagan administration's Strategic Defense Initiative) แต่ก็ไม่ได้ผลดีนัก
ในปี 1990 ห้องแลบเอกซเรย์จันทรา (Chandra X-ray Observatory) ได้เริ่มใช้งาน และได้เริ่มการสร้างรังสีเอกซ์อย่างต่อเนื่องเกิดขึ้น นำไปสู่การค้นคว้าวิจัยทางดาราศาสตร์ซึ่งเปรียบเทียบกับปรากฏการณ์ต่าง ๆ ที่เกิดขึ้น เช่น blackhole การปะทะของกาแลกซี่ nova รวมถึงดาวนิวตรอนหรือการระเบิดต่าง ๆ ที่เกิดขึ้นในเอกภพ
การประยุกต์ใช้ทางการแพทย์[แก้]
ตั้งแต่การค้นพบของ Roentgen ว่ารังสีเอกซ์สามารถบอกรูปร่างของกระดูกได้ รังสีเอกซ์ได้ถูกพัฒนาเพื่อนำมาใช้ในการถ่ายภาพในการแพทย์ นำไปสู่สาขาที่เรียกว่า รังสีวิทยา โดยนักรังสีวิทยาได้ใช้ ภาพถ่าย (radiography) ที่ได้มาใช้ในการช่วยการวินิจฉัยโรคนั่นเอง
รังสีเอกซ์มักถูกนำมาใช้ในการตรวจหาสภาพทางพยาธิวิทยาของกระดูก แต่ก็สามารถหาความผิดปกติของบางโรคที่เป็นที่เนื้อเยื่อทั่วไปได้ ตัวอย่างที่พบเห็นได้ทั่วไปเช่นการเอกซเรย์ปอด ซึ่งสามารถบอกถึงความผิดปกติได้หลายโรค เช่น โรคปอดบวม (pneumonia) โรคมะเร็งปอด (lung cancer) หรือน้ำท่วมปอด (pulmonary edema) รวมถึงการเอกซเรย์ช่องท้อง เช่นการตรวจภาวะอุดตันในลำไส้เล็ก (ileus) ภาวะลมหรือของเหลวคั่งในช่องท้อง ในบางครั้งยังใช้ในการตรวจหานิ่วในถุงน้ำดี หรือนิ่วในกระเพาะปัสสาวะได้ รวมทั้งในบางกรณีสามารถใช้ในการถ่ายภาพเนื้อเยื่อบางชนิด เช่น สมองและกล้ามเนื้อได้ แต่นับแต่ในปี 2005 รังสีเอกซ์ถูกขึ้นบัญชีในรัฐบาลสหรัฐอเมริกาว่า เป็นสารก่อมะเร็ง การถ่ายภาพเนื้อเยื่อส่วนใหญ่จึงถูกพัฒนาโดยใช้เทคนิด CAT หรือ CT scanning (computed axial tomography) หรือใช้เทคนิค MRI (magnetic resonance imaging) หรือ ultrasound ทดแทน
ปัจจุบัน การรักษาโรคมะเร็งส่วนใหญ่ได้มีการนำรังสีมาช่วยในการรักษาโรค (radiotherapy) และได้มีการรักษาพยาธิสภาพต่าง ๆ เช่น การรักษาแบบ real-time ในการผ่าตัดถุงน้ำดี การขยายหลอดเลือด (angioplasty) หรือการกลืนสาร barium enema เพื่อตรวจสภาพลำไส้เล็กและลำไส้ใหญ่ โดยการใช้ fluoroscopy
การประยุกต์ใช้ในด้านอื่น[แก้]
รังสีเอกซ์ได้ถูกพัฒนานำไปใช้ในหลายสาขา เช่น การวิเคราะห์ลักษณะของอะตอมและการผลิตโดยอาศัยการเบี่ยงเบนของรังสีเอกซ์ (x-ray crystallography) การวิจัยทางดาราศาสตร์ที่อาศัยการปลดปล่อยรังสีเอกซ์ที่มาจากวัตถุในวัตถุ (x-ray astronomy) การถ่ายภาพและผลิตภาพในขนาดเล็ก (x-ray microscopic analysis) รวมทั้งการตรวจหารอยร้าวขนาดเล็กในโลหะ การติดตามผลของตัวอย่างในการวิจัยโดยอาศัยคุณสมบัติของรังสีเอกซ์ (x-ray fluorescence) รวมถึงใช้ตรวจหาอาวุธปืนหรือระเบิดในกระเป๋าเดินทาง


 เป็นพหุนาม (เนื่องจาก
เป็นพหุนาม (เนื่องจาก  เป็นการเขียนย่อจาก
เป็นการเขียนย่อจาก  ) แต่นิพจน์
) แต่นิพจน์  ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์
ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์  เนื่องจากไม่สามารถเขียนให้อยู่ในรูปของการคูณกันที่ไม่ขึ้นกับค่าของตัวแปร
เนื่องจากไม่สามารถเขียนให้อยู่ในรูปของการคูณกันที่ไม่ขึ้นกับค่าของตัวแปร  ได้
ได้ อย่างไรก็ตาม ข้อจำกัดนี้เป็นเพียงข้อจำกัดที่ผิวเผิน เนื่องจากสามารถใช้
อย่างไรก็ตาม ข้อจำกัดนี้เป็นเพียงข้อจำกัดที่ผิวเผิน เนื่องจากสามารถใช้

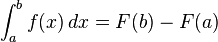

 อนุกรมของลำดับนี้ก็คือ
อนุกรมของลำดับนี้ก็คือ อนุกรมสามารถเขียนแทนได้ด้วยสัญลักษณ์ของ
อนุกรมสามารถเขียนแทนได้ด้วยสัญลักษณ์ของ

 เรานิยามให้
เรานิยามให้
 ว่าเป็น ผลรวมบางส่วน N พจน์ ของลำดับ
ว่าเป็น ผลรวมบางส่วน N พจน์ ของลำดับ 

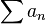
 จะเรียกว่า
จะเรียกว่า 


 แต่เมื่ออนุกรมเหล่านี้ลู่เข้าบนจำนวนจริงเสมอ การอธิบายอนุกรมก็เหมือนกับการอธิบายค่าที่แท้จริงของจำนวนนั้น (ดูเพิ่มที่
แต่เมื่ออนุกรมเหล่านี้ลู่เข้าบนจำนวนจริงเสมอ การอธิบายอนุกรมก็เหมือนกับการอธิบายค่าที่แท้จริงของจำนวนนั้น (ดูเพิ่มที่ 




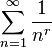

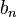 ลู่เข้าไปยังขอบเขต L ค่าหนึ่ง เมื่อ n มีค่าเข้าใกล้อนันต์ และค่าของอนุกรมนี้จะเท่ากับ
ลู่เข้าไปยังขอบเขต L ค่าหนึ่ง เมื่อ n มีค่าเข้าใกล้อนันต์ และค่าของอนุกรมนี้จะเท่ากับ 





 ถูกจำกัดขอบเขต,
ถูกจำกัดขอบเขต, 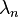 เป็นตัวจำกัดความแปรผัน และ
เป็นตัวจำกัดความแปรผัน และ  มีลิมิต
มีลิมิต

 วิธีการของอาเบลประกอบด้วยการเขียน
วิธีการของอาเบลประกอบด้วยการเขียน  และกระทำการแปลงอย่างหนึ่งซึ่งคล้ายกับ
และกระทำการแปลงอย่างหนึ่งซึ่งคล้ายกับ